1126 : Double Shortest Paths

Description

Alice and Bob are walking in an ancient maze with a lot of caves and one-way passages connecting them. They want to go from cave 1 to cave n. All the passages are difficult to pass. Passages are too small for two people to walk through simultaneously, and crossing a passage can make it even more difficult to pass for the next person. We define di as the difficulty of crossing passage i for the first time, and ai as the additional difficulty for the second time (e.g. the second person’s difficulty is d_i + a_i).

Your task is to find two (possibly identical) routes for Alice and Bob, so that their total difficulty is minimized.

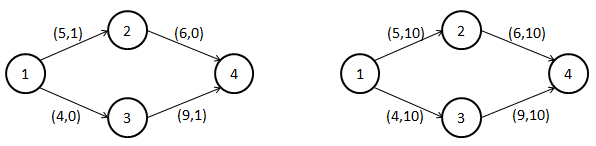
For example, in figure 1, the best solution is 1->2->4 for both Alice and Bob, but in figure 2, it’s better to use 1->2->4 for Alice and 1->3->4 for Bob.

Input

There will be at most 200 test cases. Each case begins with two integers n, m (1<=n<=500, 1<=m<=2000), the number of caves and passages. Each of the following m lines contains four integers u, v, di and ai (1<=u,v<=n, 1<=di<=1000, 0<=ai<=1000). Note that there can be multiple passages connecting the same pair of caves, and even passages connecting a cave and itself.

Output

For each test case, print the case number and the minimal total difficulty.

Sample

4 4
1 2 5 1
2 4 6 0
1 3 4 0
3 4 9 1
4 4
1 2 5 10
2 4 6 10
1 3 4 10
3 4 9 10

Case 1: 23
Case 2: 24

Hint

Source

Author

SRbGa