1132 : Just another pachinko-like machine

Description

Like pachinko? Here is another one. It’s not exactly a traditional pachinko, but it’s also a let-the-ball-hit-things game.

In the machine, there are n non-overlapping non-vertical bars, shown below.

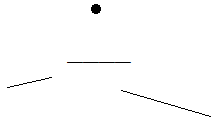
At the i-th step, the ball will be transferred to (x_i, y_i), then start to fall vertically, hopefully it’ll hit a bar and earn some scores. A ball who hit the i-th bar will earn a score of si. If the ball directly drops on the floor (with y=0), it will not score.

The most interesting part of the machine is: if the i-th bar is hit during this step, it will disappear at that moment and re-appear after d_i steps. For example, if a bar with di=3 is hit in the 5-th step, then it’ll be missing during step 6 and 7, and will re-appear in step 8.

Input

There will be at most 5 test cases. Each test case begins with one integer n (1<=n<=10⁵), the number of bars. Each of the next lines contains 5 integers x1, y1, x2, y2, s, d (0<=x1<x2<=10⁹, 1<=y1,y2<=200000, 1<=s<=1000, 1<=d<=5), describing one bar. No two bars can have any common point (i.e. no intersection, can’t touch each other etc).

Output

The next line contains b (1<=b<=10⁵), the number of balls. In the next b lines, the i-th line describes the ball appear in the i-th step. Each line contains two integers (x’, y’), that means the ball will appear at (x_i, y_i)=(x’ XOR a, y’ XOR a), where a is the current score before the ball falls (which will be zero at the beginning of each test case). It is guaranteed that xi and yi are non-negative integers and will not be precisely on a bar.

Sample

2
0 4 4 4 1 4
2 2 6 2 9 1
5
3 5
2 4
11 15
9 9
16 26
3
0 6 10 7 1 5
2 4 8 3 10 5
4 2 6 2 100 5
4
5 7
4 6
14 12
106 104

Case 1:
1
10
10
19
20

Case 2:
1
11
111
111

Hint

Explanation for Sample 1

Step 1:
ball (3,5) will hit the first bar, score=1

Step 2:
ball (3,5) will hit the second bar, score=9

Step 3(bar 2 appear again):
ball (1,5) will hit the ground, score=0

Step 4:
ball (3,3) will hit the second bar, score=9

Step 5(bar 1&2 appear again):
ball (3,9) will hit the first bar again, score=1

Source

Author

SRbGa