1190 : Complex Maze

Description

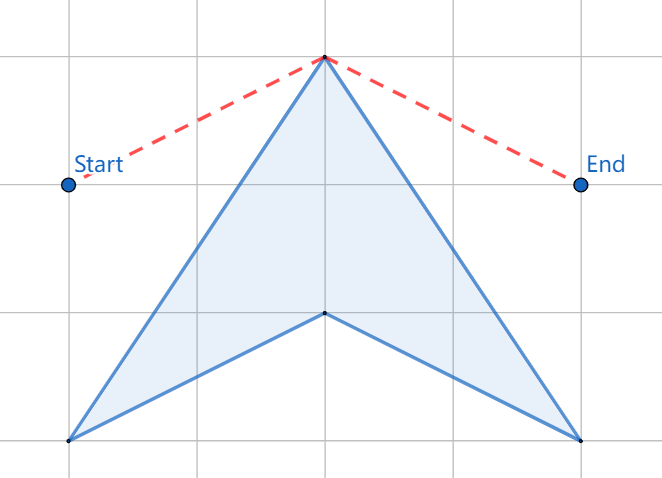
The obstacles of a maze consists of 1 simple polygon.

Given a starting point and an ending point, calculate the length of the shortest path between the two points.

Both the start and end points are outside the simple polygon (and not on vertices or edges). The path cannot pass through the obstacle area.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a flat shape consisting of straight, non-intersecting line segments or “sides” that are joined pairwise to form a single closed path. If the sides intersect then the polygon is not simple. The qualifier “simple” is frequently omitted, with the above definition then being understood to define a polygon in general.

–Wikipedia

Input

No more than 20 test cases.

For each test case, the first line is n, meaning the number of vertices in the simple polygon obstacle area.

The next n lines contain each vertex coordinate x y in counter-clockwise order.

The last two lines contain the start and end coordinates respectively.

3 ≤ n ≤ 100, all the coordinates 0 ≤ x, y ≤ 10⁴.

Output

One line for each test case, corresponding to the shortest path length from the start point to the end point.

The error from the correct answer should not exceed 10⁻⁵.

Sample

4
4 6
0 0
4 2
8 0
0 4
8 4

8.94427191

Hint

Source

Author

CSGrandeur