1228 : 彩带染色

时间限制Time Limit 2 秒Sec 内存限制Memory Limit 256 兆MB 提交次数Submitted 2 次Times 通过次数Solved 1 次Times

标准评测 Standard

从标准输入读入，结果写到标准输出。评测将输出拆成 token，与标准答案逐项比较，不按整段逐字节比对。 Read from standard input and write to standard output. The judge splits the output into tokens and compares them with the official answer; it does not compare raw bytes.

比对Compare	token 相同即通过。中间的空格、制表符、换行可多可少。Matching tokens pass. Extra spaces, tabs, or newlines between them are ignored.
不同则错Differs	token 个数或内容不同即错误。23 与 2 3、02 与 2、2.0 与 2 均视为不同。A different token count or value is wrong. 23 vs 2 3, 02 vs 2, and 2.0 vs 2 all differ.
输入Input	标准输入，格式见题面。Standard input; format as in the statement.
输出Output	标准输出。Standard output.

模板Template

C++ C Java Python

#include <iostream>
using namespace std;
int main() {
    int a, b;
    cin >> a >> b;
    cout << (a + b) << endl;
    return 0;
}

#include <stdio.h>
int main() {
    int a, b;
    scanf("%d%d", &a, &b);
    printf("%d\n", a + b);
    return 0;
}

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int a = in.nextInt();
        int b = in.nextInt();
        System.out.println(a + b);
    }
}

a, b = map(int, input().split())
print(a + b)

题目描述Description

想象一下你有一条大小为 \(n \times m\) 的大白带，初始第一列上排列着 \(n\) 支不同颜色的刷子，等待着将整条白带染成彩带。

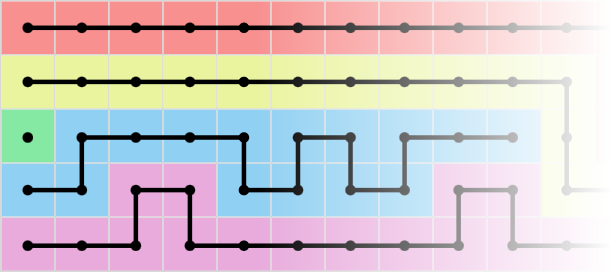
对于每支刷子，你可以将其向右、向上或向下移动多次。被经过的格子会被染上刷子的颜色，但注意每个单元格不能被重复染色，即使是颜色相同的刷子也不行。

你的目标很简单 — 使用一些操作来染色带子上的所有单元格。注意，刷子的初始位置已经染过色。

同时，由于彩带的装饰目的，对染色有一些限制。对于每个限制，其指定同一列中的两个单元格的颜色是否必须相同或不同。

在这些限制下，最终能得到多少种本质不同的彩带？请注意，在这种情况下，我们不考虑翻转或旋转彩带。

输入格式Input

第一行包含三个整数：\(n\ (1 \leq n \leq 14)\)，\(m\ (2 \leq m \leq 500)\)，\(r\ (0 \leq r \leq 500)\)，分别表示彩带的宽度、长度和限制数量。

接下来的 \(r\) 行，每行包含四个整数：\(c\ x\ y\ diff\ (1 \leq c \leq m, 1 \leq x < y \leq n, diff \in \{0, 1\})\)。这里，\(diff = 1\) 表示第 \(c\) 列中第 \(x\) 个和第 \(y\) 个单元格的颜色必须不同，否则它们必须相同。

输出格式Output

输出本质不同的彩带数量，结果对 \(998244353\) 取模。

样例Sample

出题Author

SYSU

来源Source

第九届中国大学生程序设计竞赛（秦皇岛）-（CCPC2023-Qinhuangdao）