1256 : The Only Way to the Destination

Description

There is a maze that can be represented as \(n \times m\) grids. For convenience, we define \((x,y)\) as the grid in the \(x\)-th row and \(y\)-th column.

Initially, every grid is empty. Alice wants to design this maze. So she will place \(k\) walls in the grids. Each wall is represented as \(x_1,x_2,y\), where it means that \(\forall x_1\le i \le x_2\), \((i, y)\) will becomes a part of this wall and cannot be passed by. Except wall grids, all of the other grids are empty. Alice ensures that after placing \(k\) walls, all empty grids remain connected and the maze has at least one empty grid. And it is guaranteed that different walls have no common grids.

Now, Alice want to know, does any pair of empty grids have only one simple path connecting them?

If your are not familar with the definition of “simple path”, here is it:

A simple path connecting empty grids \((x_s,y_s)\) and \((x_d,y_d)\) is defined as a sequence of grid positions \(S=\{(x_1,y_1),(x_2,y_2)\cdots (x_{len},y_{len})\},(len\ge 2)\) that satisfies the following conditions:

• \((x_1,y_1)=(x_s,y_s),(x_{len},y_{len})=(x_d,y_d)\)
• \(\forall 1\le i \le len,\ 1\le x_i \le n,1\le y_i\le m\)
• \(\forall 1\le i \le len\), \((x_i,y_i)\) is an empty grid
• \(\forall 1\le i \le len-1,\ |x_i-x_{i+1}|+|y_i-y_{i+1}| = 1\)
• \(\forall 1\le i < j\le len, (x_i,y_i)\neq (x_j,y_j)\)

If any two different empty grids \((x_s,y_s),(x_d,y_d),\{ (x_s,y_s)\ne (x_d,y_d)\}\) have exactly one simple path connecting them, output YES. Otherwise, output NO.

Input

The first line contains three integers \(n, m, k(1\le n, m \le 10^9, 1\le k \le 10^5)\), indicating the number of rows, the number of columns, and the number of walls.

For the next \(k\) lines, each line contains three integers \(x_1,x_2,y(1\le x_1\le x_2\le n, 1\le y\le m)\) indicating a wall placed in the maze.

It is guaranteed that each pair of empty grids has at least one simple path connecting them.

Output

Output a string to represent the answer, YES or NO.

Sample

5 3 2
2 5 1
1 4 3
##CASE##
5 3 1
2 4 2
##CASE##
2 4 2
2 2 1
1 1 4

YES

##CASE##
NO
##CASE##
NO

Hint

Sample explanations contains Alice’s maze, with yellow squares representing walls and white squares representing empty grids.

1. In the first example, we can observe that regardless of the choice of starting and ending grid, there is only one simple path.

2. In the second example, choose \((1,1)\) as the starting grid and \((5,1)\) as the destination grid. \(S_1=\{(1,1)\), \((2,1)\), \((3,1)\), \((4,1)\), \((5,1)\}\) and \(S_2=\{(1,1)\), \((1,2)\), \((1,3)\), \((2,3)\), \((3,3)\), \((4,3)\), \((5,3)\), \((5,2)\), \((5,1)\}\) are two different simple paths.

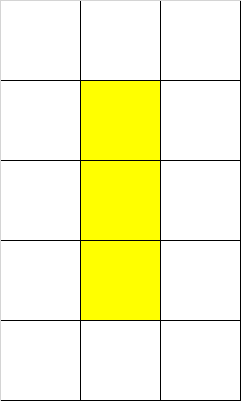
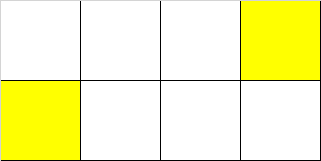
3. In the third example, choose \((1,2)\) as the starting grid and \((2,3)\) as the destination grid. \(S_1=\{(1,2)\), \((1,3)\), \((2,3)\}\) and \(S_2=\{(1,2)\), \((2,2)\), \((2,3)\}\) are two different simple paths.

Source

Author

FUDAN