1277 : 田字格

Description

小 I 正在学习练字，可当他打开白纸时才想起来自己之前无聊在白纸上将 \(n\) 条线段涂黑了，纸上其他部分都是白的。

这 \(n\) 条被涂黑的线段都是水平的或者竖直的：以白纸中心为原点，平行白纸的某条边构建 \(x\) 轴，另一条边构建 \(y\) 轴，那么每条被涂黑的线段的两个端点 \((x_1,y_1)\) 和 \((x_2,y_2)\) 满足：\(x_1 = x_2\) 和 \(y_1 = y_2\) 恰有一个成立。同时，任意两条水平的线段没有交点，任意两条竖直的线段没有交点。

尽管涂黑的线段很让小 I 糟心，深谙福祸相依的小 I 还是发现，涂黑的 \(n\) 条线段构成了若干田字格，而他可以在这些田字格上练字。

田字格可以由三元组 \((x_0, y_0, d)\) 描述。一个三元组 \((x_0, y_0, d)\) 是田字格当且仅当以下条件成立：

• \(x_0, y_0 \in \mathbb{R}\), \(d \in \mathbb{R}^+\)；
• 设 \(R = [x_0-d,x_0+d] \times [y_0-d,y_0+d]\)，即横坐标在 \([x_0-d,x_0+d]\) 内、纵坐标在 \([y_0-d,y_0+d]\) 内的所有点。那么 \(R\) 中被涂黑的部分恰好构成六条线段，且这六条线段分别是 \(x=x_0-d,x=x_0,x=x_0+d,y=y_0-d,y=y_0,y=y_0+d\) 这六条直线与 \(R\) 的交。

小 I 于是想想算算白纸上有几个田字格，也就是有多少个满足以上条件的三元组 \((x_0,y_0,d)\)。但按照惯例小 I 不会算，所以这个任务交给了你。

Input

输入的第一行一个整数 \(n (1 \le n \le 3 \times 10^5)\) 表示线段数。接下来 \(n\) 行每行四个整数 \(x_1,y_1,x_2,y_2 (-10^9 \le x_1 \le x_2 \le 10^9, -10^9 \le y_1 \le y_2 \le 10^9)\) 表示一条线段。

输入的每条线段满足 \(x_1 = x_2\) 和 \(y_1 = y_2\) 恰有一个成立，且任意两条满足 \(x_1 = x_2\) 的线段间没有交点，任意两条满足 \(y_1 = y_2\) 的线段间没有交点。

Output

输出一行一个整数表示田字格的数量。

Sample

10
-10 -10 -10 10
0 -10 0 10
10 -10 10 10
-10 -10 10 -10
-10 0 10 0
-10 10 10 10
5 -10 5 10
-10 5 10 5
-2 0 -2 10
-5 -5 10 -5

3

Hint

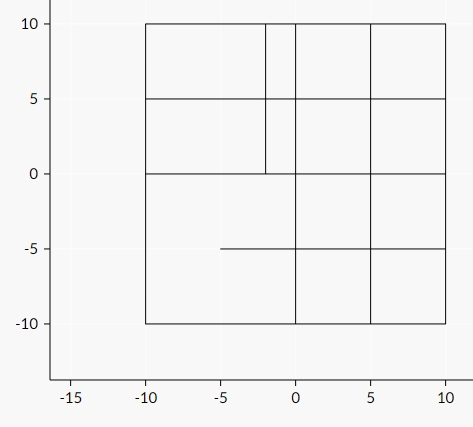
如上图所示，\((5, 5, 5), (5, 0, 5), (5, -5, 5)\) 是三个合法的田字格。注意以下几个都不是田字格：

• \((0, 0, 10)\)，因为除了需要的六条线段以外还有其他部分被涂黑了；
• \((-5, 5, 5)\)，因为 \(x=-5\) 与正方形的交没有被涂黑。

Source

Author

THU